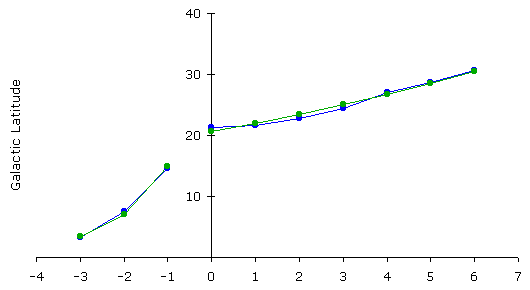To read this webpage in English
Click Here

Прецессия планет

или

О чём писал Платон?

В.Л. Пахомов

Часть вторая

Закон прецессии системы планет

"Главная цель всех исследований внешнего мира должна состоять в том,
чтобы обнаружить рациональный порядок и гармонию,
которая была наложена на это богом,
и которую он открыл нам на языке математики."
— Иоганн Кеплер (1571-1630)

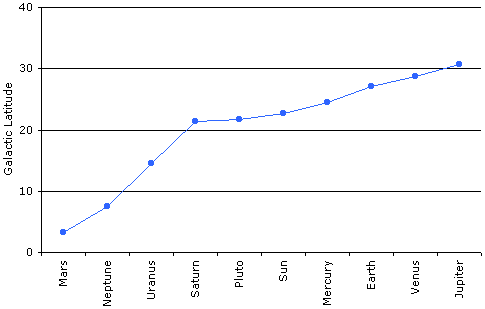
Теперь перейдём к анализу галактической широты северного полюса планет (см. табл. 1).

Так как нас интересует только угол наклона осей вращения планет к плоскости Галактики, а не куда смотрит северный полюс, то у Плутона можно поменять знак галактической широты, то есть использовать широту южного полюса (тем более что он имеет обратное вращение).

В следующей таблице планеты упорядочены по возрастанию угла наклона их оси вращения к плоскости Галактики.

Таблица 3

Эти данные представлены на следующем графике.

Рисунок 8

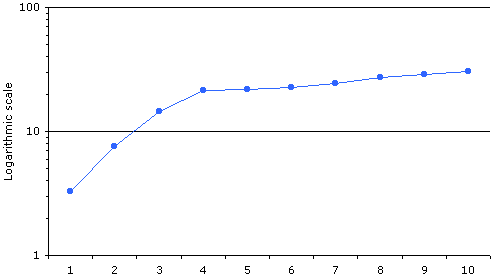
Для отыскания аналитической формы этой зависимости представим те же данные на логарифмической шкале.

Рисунок 9

Как видно, два прямых участка этого графика [1, 3] и [4, 10] допускают аппроксимацию функцией вида b = a·p^k.

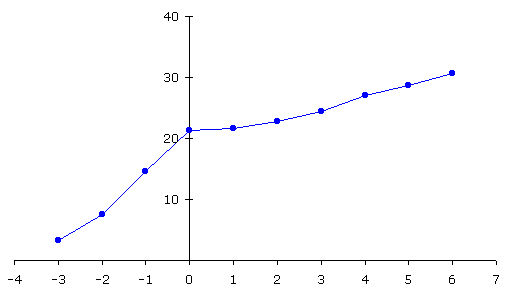
Если перенести начало координат в точку (4, 0), то исходный график будет выглядеть так.

Рисунок 10

Здесь чётко выделены два участка. Обратите внимание, что Платон также берёт две последовательности чисел.

Используя метод наименьших квадратов, получаем значения параметров a и p

b_k = a·p^k , k = 0, 1,... ,6

где:

a = a₁ = 20.5839, p = p₁ = 1.0673

для группы семи планет (рис. 10).

Для группы четырёх планет (k = -3, -2, -1, 0) будет такой же вид зависимости, но с коэффициентами

a = a₂ = 24.006, p = p₂ = 1.876

Коэффициент p₂ близок к 2, как и указал Платон, дав ряд геометрической прогрессии (2, 4, 8) с коэффициентом 2.

Аппроксимация по первым трём планетам (k = -3, -2, -1) даёт коэффициент p_2' = 2.109, что ещё ближе к 2.

На следующем графике показано полученное приближение.

Рисунок 11

Здесь исходные данные изображены синим цветом. Средняя относительная погрешность равна 2.43%.

Учитывая данные древней науки, остатки которой изложены Платоном, и видя, что указанная зависимость сохраняется и в наши дни, можно утверждать, что в ходе прецессии планет значения коэффициентов p₁ и p₂ остаются постоянными.

Коэффициенты p₁ и p₂ можно назвать гармоническими постоянными прецессии.

Этот закон позволяет рассчитать параметры прецессии всех планет и Солнца, зная данные о прецессии одной планеты (например, Земли).

Далее я изложу сведения, ведущие к более глубокому пониманию коэффициентов p₁ и p₂.

Диатоническая Солнечная система

"...уши народа, населяющего летучий остров [Лапута],
одарены способностью воспринимать музыку сфер..."
— Джонатан Свифт (1667-1745)

Теория, что планеты при своём вращении вокруг Земли производят определённые звуки, отличающиеся друг от друга в зависимости от величины, быстроты движения тел и их удаления была общепринятой у греков в древности.

Пифагор и его последователи, а позже и Кеплер верили, что вселенная полностью организована по системе музыкальной гармонии. Для них все во вселенной вибрировало в гармонии с большими телами, и мы буквально живем внутри этого гигантского музыкального инструмента, который играет ноты, аккорды и гаммы. В 1619 году Иоганн Кеплер опубликовал книгу "Harmonice Mundi" (Гармония Мироздания). Это была попытка Кеплера связать музыкальную гармонию с планетарным движением и, более определенно, найти "музыкально-гармоничное" отношение между расстояниями планет от Солнца.

Монохорд вселенной Роберта Флудда, 1627 г.

Музыкальная диатоническая шкала имеет древнее происхождение, но специфическая настройка была включена в современный чистый строй благодаря Клавдию Птолемею (греч. астроном, ок. 100 - ок. 170 г.). Он дал её как одну из дюжины возможных настроек диатонической шкалы, назвав её "синтоническая диатоническая".

В диатонической шкале есть три интервала: ⁹/₈ (1.125), ¹⁰/₉ (1.111), и ¹⁶/₁₅ (1.067). Первые два называют целыми тонами, а третий — полутоном.

Как вы можете видеть, коэффициент p₁ = 1.0673, полученный в главе "Закон прецессии системы планет", действительно совпадает с коэффициентом (интервалом) диатонической музыкальной шкалы (полутон)!

Упоминаемые Платоном интервалы (определяющие структуру сфер, составляющих космос), в музыке называются: ³/₂ - квинта, ⁴/₃ - кварта, ⁹/₈ - секунда. А дробь ²⁵⁶/₂₄₃ = 1.0535... является основой построения современной музыкальной шкалы — темперированного строя, созданного лишь через 2000 лет после Платона [2].

Современная музыка использует темперированную шкалу с коэффициентом ¹²√2 = 1.0595... Соответствующий звуковой интервал называется полутоном. Равномерная темперация делает отношение между каждым полутоном константой. Я писал об этом в книге [3].

В 1722 году, И.С. Бах, узнав о равномерной двенадцатитоновой музыкальной шкале, описанный в 1691 году немецким учёным и музыкантом Андреасом Веркмейстером (1645-1706), написал опус "Хорошо темперированный клавир". Это был первый в истории музыки опыт применения темперированного строя.

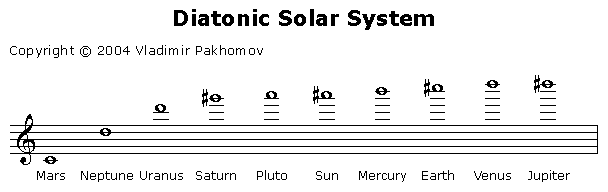
Таким образом, если принять что Марс соответствует ноте 'до' 1-й октавы, то на современной музыкальной шкале планеты расположатся так:

Рисунок 12

Всё это звучит одновременно, одним аккордом. Знак альтерации — # (диез), означает на полутон выше. Например, #до — читается 'до диез' и т.д.

Рисунок 12 является музыкальной аппроксимацией графика галактической широты северного полюса планет (см. рис. 8). Более того, аппроксимации, показанные на рисунках 11 и 12, полностью эквивалентны в их числовом выражении.

Исходя из вышеизложенного, можно сказать, что все 10 "планет" занимают диапазон в 4 октавы на музыкальной шкале.

• 1-я октава: до — Марс;

• 2-я октава: ре — Нептун;

• 3-я октава: ре — Уран, #соль — Сатурн, ля — Плутон, #ля — Солнце, си — Меркурий;

• 4-я октава: #до — Земля, ре — Венера, #ре — Юпитер.

Таким образом, пифагорейская "гармония" и "музыка сфер" выражают реальный закон небесной механики.

Какая сила заставляет планеты прецессировать в соответствии с музыкальной шкалой, а солнечную систему организовала как хорошо настроенный инструмент?

Продолжение (см. Часть третья)

Спасибо за посещение моего сайта