Владимир Пахомов   Книга, запечатанная семью печатями   Расшифровка Послания неизвестной высокоразвитой цивилизации ЧАСТЬ ПЕРВАЯ (Краткое изложение первой части книги "Тайна Календаря")

"История, это обширная система раннего предупреждения"

— Norman Cousins

Календарь пришел к нам из Древнего Египта и мы все еще используем его. Это календарь, базирующийся на Сотис (звезда Сириус). Египетские фараоны должны были давать клятву никогда не изменять календарь. Этот Древний календарь, по существу, является единственным разумным календарем во всей человеческой истории. Его математический алгоритм определяется двумя циклами:

• 4-летний цикл високосных лет;

• 7-дневный цикл недель.

Оба эти цикла известны с древнейших времен.

Одно из известных нам описаний четырехлетнего цикла было найдено в Канопском декрете.

Канопский декрет (каменная плита с трехъязычной надписью,
238 г. до н.э., Египет). Часть греческой надписи.

"...так как восход Божественной Сотис¹ в течении четырех лет уходит на один день... если год будет и впредь состоять из 360 дней и пяти дней к ним добавляемых, отныне будет после каждых четырех лет добавляться один день, как праздник Богов Благодетелей², к пяти добавочным дням перед Новым Годом..."

¹ Божественная Сотис ― звезда Сириус.

² Боги Благодетели ― царь Птолемей III Эвергет и его жена Вереника.

Это правило, также было введено в календарь Селевкидов, принятом в 312 г. до н.э.

Происхождение семидневного цикла также относится к глубокой древности. Например, деление года на пятьдесят две недели по семь дней каждая, ясно указано в тексте Книги Юбилеев. Она утверждает, что когда Потоп закончился, Ною были даны "небесные плитки" предписывающие, что

"Всех дней, которые предписаны, пятьдесят две недели дней; этим весь год исполняется. Так начертано и установлено на небесных плитках..."

Христианский, еврейский и мусульманский календари все имеют 7-дневную неделю. Нет ни одной записи, что 7-дневный цикл недели когда-либо был нарушен. Изменения и реформы календаря никогда не прерывали 7-дневный цикл.

Две главные версии Древнего календаря существуют в настоящее время: Юлианский календарь и Григорианский календарь.

Когда римский полководец Гай Юлий Цезарь прибыл в Египет в 48 г. до н.э., он был так впечатлен Египетским календарем, что решил ввести его в Римской империи. Он провел его знаменитую календарную реформу в 45 г. до н.э. После этого Древний календарь стал известен, как Юлианский.

Календарь принятый Юлием Цезарем был идентичен Александрийскому календарю Аристарха 239 г. до н.э. Он состоял из солнечного года 12-ти месяцев и 365 дней с дополнительным днем каждые четыре года.

Юлианский календарь использовался европейскими странами более 1500 лет. Например, Православная церковь в России все еще использует его.

Календарная реформа папы Григория XIII (1582 г.) добавила одно дополнительное правило в Древний календарь, чтобы увеличить его точность.

В Юлианском календаре действует правило:
"год, который делится на 4 ― високосный".

Григорианская реформа добавила:
"кроме случаев, когда год делится на 100 и не делится на 400".

Поэтому 1600 и 2000 годы високосные, а 1700, 1800, 1900 и 2100 год не високосные. Но в Юлианском календаре эти годы високосные. И в каждом таком случае, разница в датах между Юлианским и Григорианским календарями увеличивается на один день. В этом вся разница между ними.

Отсюда видно, что это не какой-то новый "Григорианский" календарь, а всего лишь Григорианская поправка к Древнему календарю. Я не использую эту поправку в расшифровке Календарного Послания.

Далее я буду использовать Юлианский календарь мартовского стиля (т.е. новый год начинается 1 марта, а дополнительный день, 29 февраля, вставляется в конце високосного года).

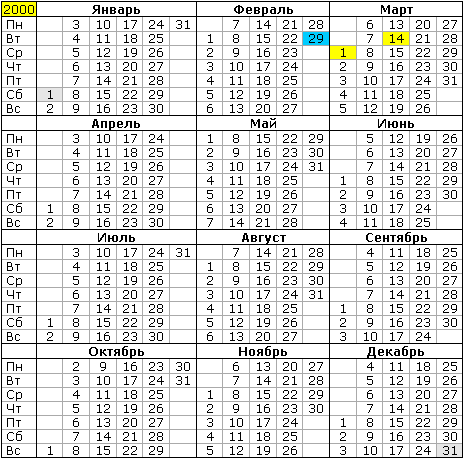
В нашем календаре используются годы и дни. Год и день, естественные деления времени. Вместе с этой системой, концепция "недель" группирует дни в наборы по 7. Как это можно объяснить? Семидневная неделя не является естественным делением времени.

Посмотрите на календарь 2000 года.

2000 год был високосным (с високосным днем ― 29 февраля). Я взял этот обычный Григорианский календарь (январского стиля) для наглядного пояснения следующих календарных правил.

Правило 1: Високосный год имеет 366 дней или 52 недели и 2 дня. Первый день 2000-го года ― суббота, а последний день ― воскресенье (то есть, следующий день недели). День недели последнего дня високосного года является следующим за днем недели его первого дня.

Правило 2: Простой (не високосный) год имеет 365 дней или 52 недели и 1 день. Например, 2003 год ― простой. Он начинается в среду, и заканчивается в среду. Любой простой год начинается и заканчивается в одинаковый день недели.

Правило 3: Вся последовательность лет делится на группы по 4 года: 3 простых года, 1 високосный; 3 простых года, 1 високосный; и т.д.

В Юлианском календаре связь между днями недели и датами года повторяется в цикле 28 лет. Этот период называется 28-летним Солнечным циклом. Используя правила 1, 2 и 3 можно записать таблицу Солнечного цикла, позволяющую легко определить календарь на любой год (и для Григорианского календаря тоже).

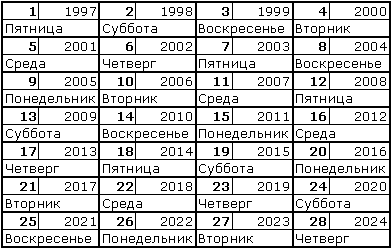
Таблица 1

В каждой клетке таблицы 1 показаны:

• Порядковый номер года в Солнечном цикле;

• Год;

• День недели первого дня года (1 марта).

Далее все повторяется. То есть календарь на 2025 год полностью совпадет с календарем на 1997 год; календарь на 2026 год совпадет с календарем на 1998 год и т.д.

Все високосные годы расположены в третьем столбце таблицы 1.

Я не случайно начал таблицу 1 с 1997 года. Это первый год 269-го Солнечного цикла. Счет Солнечных циклов ведется с 1 марта (пятница) 5508 г. до н.э. Это эра "от сотворения мира" или древнерусская эра. Все проекты «вечных» календарей используют таблицу 1. Таблица Солнечного цикла использовалась ещё до нашей эры.

Известные анализы структуры календаря заканчиваются на этом, но мое исследование только начинается.

Календарное Послание

В течение неисчислимых столетий, исторические и эзотерические источники передавали рассказы о забытой "капсуле" древних знаний. Древнеегипетский бог Тот, перед его возвращением на небеса, сказал:

"О вы, священные книги... оставайтесь нетленными в течение веков и будьте невидимы и необнаружимы для всех людей, которые станут ходить по равнинам этой земли до тех пор, пока Небеса, постарев, не породят организмов, достойных вас."

Эта цитата говорит, что будущие поколения найдут и прочитают книги Тота.

Следующая цитата также говорит о книге, написанной для будущих поколений.

"И он сказал мне: "Изучай, Енох, эти небесные плитки, и читай то, что написано на них... Я знаю тайну, и читал небесные плитки... и написал о них... но не для этого поколения, а для отдалённого, которое придёт."

— Книга Еноха

Древняя Книга Еноха была запрещена, утеряна и забыта на тысячи лет. Эта книга рассказывает, как "ангелы, сыны небесные... И всех их было двести" спустились на землю.

В сущности, тайны, которые были переданы Еноху, а им его сыновьям для хранения и передачи будущим поколениям, были календарными знаниями. Что же было скрыто в календаре для будущих поколений?

Продолжение (см. Часть вторая)

Copyright © 2000 В.Л.Пахомов

Никакая часть этой статьи не может воспроизводиться или передаваться,
в любой форме или любым средством, без предварительного разрешения автора.

Обновлено: 16 августа 2014 г.